анотація
Використовувані терміни: Нехай X і Y - два безлічі. Закон F, згідно з яким кожному елементу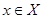 
поставлений у відповідність єдиний елемент 
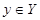, Називається відображенням множини X в безліч Y або функцією, заданою на X зі зна
нями в Y. Максимум - максимальне або мінімальне значення функції на заданій множині. Завдання безумовної оптимізації полягає в знаходженні мінімуму або максимуму функції за відсутності будь-яких обмежень. Умовна оптимізація - пошук мінімуму або максимуму функції при наявності обмежень. Безумовна оптимізація - пошук мінімуму або максимуму функції без наявності активних обмежень. Послідовність певних і невід'ємних функцій на безлічі називають штрафом або штрафний функцією. Ітераційний процес - багаторазово повторювані дії (обчислення) до виконання деякого умови закінчення. Цільова функція - функція, що зв'язує мета (що оптимізуються змінну) з керованими змінними в задачі оптимізації.
У даній роботі вирішується завдання пошуку екстремуму (максимуму) функції декількох змінних при наявності обмеження рівності. Для вирішення використовується метод штрафних функцій, який дозволяє звести задачу пошуку умовного екстремуму до вирішення послідовності завдань на пошук безумовного екстремуму допоміжної функції.
число сторінок
22
число малюнків
9
число таблиць
2
число додатків
2
Зміст
Вступ
1. Основна частина
1.1 Постановка завдання
1.2 Аналіз завдання
1.3 Опис методу штрафних функцій
1.4 Графічне рішення задачі
1.5 Формалізація розрахунків
2. Структура програми, призначеного для вирішення завдання
3. Результати обчислень
4. Висновки
5. Список літератури
6. Додатки
Вступ
Математичне програмування - математична дисципліна, що вивчає теорію і методи вирішення завдань про знаходження екстремумів функції на множинах конечномерного векторного простору, що визначаються лінійними і нелінійними обмеженнями (рівностями і нерівностями). Залежно від природи множин завдання математичного програмування класифікуються як:
· Завдання дискретного програмування (або комбінаторної оптимізації) - якщо безліч звичайно і лічильно;
· Задачі цілочислового програмування - якщо безліч є підмножиною множини цілих чисел;
· Завдання лінійного програмування - якщо всі обмеження і цільова функція містять лише лінійні функції;
· Завдання нелінійного програмування - якщо обмеження або цільова функція містять нелінійні функції і безліч є підмножиною конечномерного векторного простору.
Оптимізація - цілеспрямована діяльність, яка полягає в отриманні найкращих результатів при відповідних умовах.
Математичне програмування використовується при вирішенні оптимізаційних задач дослідження операцій. Спосіб знаходження екстремуму повністю визначається класом поставленого завдання.
У даній роботі поставлена задача умовної оптимізації, тобто задача, яка містить деякі обмеження по незалежним змінним на безлічі G. Ці обмеження задаються сукупністю деяких функцій, що задовольняють равенствам або нерівностей. Обмеження - рівності виражають залежність між проектними параметрами, яка повинна враховуватися при знаходженні рішення. Обмеження-нерівності встановлюють менш жорсткі залежності між проектними параметрами, дозволяючи їм в деякій частині області G залишатися незалежними, а в іншій частині проявляється залежність один від одного. Рішення завдання умовної оптимізації часто можна знайти, використовуючи аналітичні методи рішення, тому потрібно використання додаткових чисельних методів.
В даний час розроблено безліч чисельних методів для задач як безумовної, так і умовної оптимізації.
Методи умовної оптимізації, як правило, зводять рішення вихідної задачі до багаторазового вирішення допоміжної задачі безумовної оптимізації.
Рішення безумовної оптимізації є більш простим і легко реалізується в сучасних математичних пакетах. Для вирішення поставленого завдання використовувалися кошти програми MathCAD. Дана програма дозволяє виконати як чисельні, так і аналітичні обчислення, має зручний математично-орієнтований інтерфейс і прекрасні засоби графіки. Система MathCAD спочатку створювалася для чисельного розв'язання математичних задач, пізніше в неї були інтегровані інструменти символьної математики з системи Maple, що поступово перетворило MathCAD в універсальний інструмент вирішення математичних задач. Тому вибір даного програмного засобу цілком обгрунтований.
1. Основи частина
1.1 Постановка завдання
Потрібно знайти точку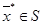 
таку, що
f (x *) = x1 - 2x22 + 4x2 → max (1)
де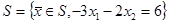 
(2)
за допомогою методу штрафних функцій.
1.2 Аналіз завдання
Дане завдання відноситься до класу задач нелінійного програмування. Вирішується методом штрафних функцій. Цей метод полягає в зведенні задачі, на умовний екстремум, до вирішення послідовності завдань на пошук безумовного екстремуму допоміжної функції, яка буде складена по нижчеописаних методів. Рішення нового завдання проведемо двома методами безумовної оптимізації різного порядку. Для даного проекту було обрано метод сполучених напрямків, який є методом нульового порядку, і метод найшвидшого градієнтного спуску, що є методом першого порядку.
Недоліком методу найшвидшого спуску є його низька ефективність в оптимізації ярів функцій. Застосування даного методу допустимо, так як функція неперервна на всій області визначення (областю визначення функції є вся площину (x1, x2)), і безперервні її приватні похідні першого порядку:
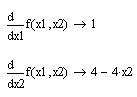
Обидва методи безумовної оптимізації зводять задачу пошуку найменшого значення функції кількох змінних до багаторазового вирішення одновимірних задач оптимізації. Метод найшвидшого градієнтного спуску гарантує збіжність до точки мінімуму для сільновипуклих функцій. При зменшенні нерівності зменшується і швидкість збіжності ітераційного процесу. Якщо потрібно знайти глобальний мінімум функції, то для строго опуклою функції рішення цього завдання аналогічно пошуку локального мінімуму. Якщо є кілька мінімумів, пошук глобального мінімуму зводиться до перебору всіх локальних мінімумів. У методі сполучених напрямків використовується той факт, що мінімум квадратичної функції може бути знайдений не більше ніж за n кроків за умови, що пошук ведеться уздовж пов'язаних щодо матриці Гессе напрямків. Так як досить великий клас цільових функцій може бути представлений в околиці точки мінімуму квадратичної аппроксимацией, описана ідея застосовується і для неквадратічних функцій. Вихідна функція є строго опуклою і, відповідно, має тільки один мінімум, що виправдовує вибір методів для пошуку безумовного екстремуму. Методи безумовної оптимізації можна оцінити за такими параметрами:
Сторінка: 1 2 3 4
