анатацыя
Выкарыстоўваюцца тэрміны: Няхай X і Y - два мноства. Закон F, згодна з якім кожнаму элементу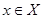 
пастаўлены ў адпаведнасць адзіны элемент 
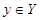, Называецца адлюстраваннем мноства X ст мноства Y ці функцыяй, зададзенай на X са знач
ниями ў Y. экстрэмуму - максімальнае або мінімальнае значэнне функцыі на зададзеным мностве. Задача безумоўнай аптымізацыі складаецца ў знаходжанні мінімуму або максімуму функцыі ў адсутнасць якіх-небудзь абмежаванняў. Умоўная аптымізацыя - пошук мінімуму або максімуму функцыі пры наяўнасці абмежаванняў. Безумоўная аптымізацыя - пошук мінімуму або максімуму функцыі без наяўнасці актыўных абмежаванняў. Паслядоўнасць вызначаных і неадмо ¢ ных функцый на мностве называюць штрафам або штрафной функцыяй. Ітэрацыйныя працэс - шматкроць паўтараюцца дзеянні (вылічэнні) да выканання некаторага ўмовы заканчэння. Мэтавая функцыя - функцыя, якая злучае мэта (оптимизируемую зменную) з кіраванымі зменнымі ў задачы аптымізацыі.
У дадзенай працы вырашаецца задача пошуку экстрэмуму (максімуму) функцыі некалькіх зменных пры наяўнасці абмежаванні роўнасці. Для вырашэння выкарыстоўваецца метад штрафных функцый, які дазваляе звесці задачу пошуку ўмоўнага экстрэмуму да вырашэння паслядоўнасці задач на пошук безумоўнага экстрэмуму дапаможнай функцыі.
колькасьць старонак
22
лік малюнкаў
9
лік табліц
2
лік прыкладанняў
2
змест
ўвядзенне
1. Асноўная частка
1.1 Пастаноўка задачы
1.2 Аналіз задачы
1.3 Апісанне метаду штрафных функцый
1.4 Графічнае рашэнне задачы
1.5 Фармалізацыя разлікаў
2. Структура прыкладання, прызначанага для рашэння задачы
3. Вынікі вылічэнняў
4. Высновы
5. Спіс літаратуры
6. Прыкладанні
ўвядзенне
Матэматычнае праграмаванне - матэматычная дысцыпліна, якая вывучае тэорыю і метады рашэння задач аб знаходжанні экстрэмуму функцыі на мноствах канечнамернае вектарнага прасторы, якiя вызначаюцца лінейнымі і нелінейнымі абмежаваннямі (роўнасць і няроўнасць). У залежнасці ад прыроды мностваў задачы матэматычнага праграмавання класіфікуюцца як:
· Задачы дыскрэтнага праграмавання (або камбінаторныя аптымізацыі) - калі мноства вядома і лічыльна;
· Задачы цэлалікавага праграмавання - калі мноства з'яўляецца падмноствам мноства цэлых лікаў;
· Задачы лінейнага праграмавання - калі ўсе абмежаванні і мэтавая функцыя ўтрымліваюць толькі лінейныя функцыі;
· Задачы нелінейнага праграмавання - калі абмежаванні або мэтавая функцыя ўтрымліваюць нелінейныя функцыі і мноства з'яўляецца падмноствам канечнамернае вектарнага прасторы.
Аптымізацыя - мэтанакіраваная дзейнасць, якая складаецца ў атрыманні найлепшых вынікаў пры адпаведных умовах.
Матэматычнае праграмаванне выкарыстоўваецца пры вырашэнні аптымізацыйных задач даследавання аперацый. Спосаб знаходжання экстрэмуму цалкам вызначаецца класам пастаўленай задачы.
У дадзенай працы пастаўлена задача ўмоўнай аптымізацыі, г.зн. задача, якая змяшчае некаторыя абмежаванні па незалежным пераменным на мностве G. Гэтыя абмежаванні задаюцца сукупнасцю некаторых функцый, якія задавальняюць роўнасць або няроўнасць. Абмежаванні - роўнасці выказваюць залежнасць паміж праектнымі параметрамі, якая павінна ўлічвацца пры знаходжанні рашэння. Абмежаванні-няроўнасці усталёўваюць менш жорсткія залежнасці паміж праектнымі параметрамі, дазваляючы ім у некаторай частцы вобласці G заставацца незалежнымі, а ў астатняй частцы праяўляецца залежнасць адзін ад аднаго. Рашэнне задачы ўмоўнай аптымізацыі часцяком нельга знайсці, выкарыстоўваючы аналітычныя метады рашэння, таму патрабуецца выкарыстанне дадатковых лікавых метадаў.
У цяперашні час распрацавана мноства лікавых метадаў для задач як безумоўнай, так і ўмоўнай аптымізацыі.
Метады ўмоўнай аптымізацыі, як правіла, зводзяць рашэнне зыходнай задачы да шматразовага рашэнню дапаможнай задачы безумоўнай аптымізацыі.
Рашэнне безумоўнай аптымізацыі з'яўляецца больш простым і лёгка рэалізуецца ў сучасных матэматычных пакетах. Для вырашэння пастаўленай задачы выкарыстоўваліся сродкі праграмы MathCAD. Дадзеная праграма дазваляе выканаць як лікавыя, так і аналітычныя вылічэнні, мае зручны матэматычна-арыентаваны інтэрфейс і выдатныя сродкі графікі. Сістэма MathCAD першапачаткова стваралася для колькаснага рашэння матэматычных задач, пазней у яе былі інтэграваныя інструменты знакавай матэматыкі з сістэмы Maple, што паступова ператварыла MathCAD ў універсальны інструмент вырашэння матэматычных задач. Таму выбар дадзенага праграмнага сродкі цалкам абгрунтаваны.
1. Асновы частка
1.1 Пастаноўка задачы
Патрабуецца знайсці кропку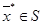 
такую, што
f (x *) = x1 - 2x22 + 4x2 → max (1)
дзе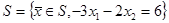 
(2)
з дапамогай метаду штрафных функцый.
1.2 Аналіз задачы
Дадзеная задача ставіцца да класа задач нелінейнага праграмавання. Вырашаецца метадам штрафных функцый. Гэты метад заключаецца ў звядзенні задачы, на ўмоўны экстрэмуму, да вырашэння паслядоўнасці задач на пошук безумоўнага экстрэмуму дапаможнай функцыі, якая будзе складзена па нижеописанным метадам. Рашэнне новай задачы правядзем двума метадамі безумоўнай аптымізацыі рознага парадку. Для гэтага праекта былі выбраны метад спалучаных кірункаў, які з'яўляецца метадам нулявога парадку, і метад найхутчэйшага градыентнага спуску, які з'яўляецца метадам першага парадку.
Недахопам метаду найхутчэйшага спуску з'яўляецца яго нізкая эфектыўнасць у аптымізацыі ярава функцый. Прымяненне дадзенага метаду дапушчальна, так як функцыя бесперапынная на ўсёй вобласці вызначэння (вобласцю вызначэння функцыі з'яўляецца ўся плоскасць (x1, x2)), і бесперапынна яе прыватныя вытворныя першага парадку:
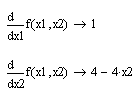
Абодва метаду безумоўнай аптымізацыі зводзяць задачу пошуку найменшага значэння функцыі некалькіх зменных да шматразовага рашэнню аднамерных задач аптымізацыі. Метад найхутчэйшага градыентнага спуску гарантуе збежнасць да кропкі мінімуму для сильновыпуклых функцый. Пры памяншэнні выпукласці памяншаецца і хуткасць збежнасці ітэрацыйныя працэсу. Калі патрабуецца знайсці глабальны мінімум функцыі, то для строга выпуклай функцыі рашэнне гэтай задачы аналагічна пошуку лакальнага мінімуму. У выпадку існавання некалькіх мінімумаў, пошук глабальнага мінімуму зводзіцца да перабору ўсіх лакальных мінімумаў. У метадзе спалучаных кірункаў выкарыстоўваецца той факт, што мінімум квадратычнай функцыі можа быць знойдзены не больш чым за n крокаў пры ўмове, што пошук вядзецца уздоўж спалучаных адносна матрыцы Гесэ кірункаў. Так як досыць вялікі клас мэтавых функцый можа быць прадстаўлены ў наваколлі кропкі мінімуму квадратычнай апраксімацыі, апісаная ідэя ўжываецца і для неквадратичных функцый. Зыходная функцыя з'яўляецца строга выпуклай і, адпаведна, мае толькі адзін мінімум, што апраўдвае выбар метадаў для пошуку безумоўнага экстрэмуму. Метады безумоўнай аптымізацыі можна ацаніць па наступных параметрах:
Старонка: 1 2 3 4
